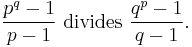Feit–Thompson conjecture

In mathematics, the Feit–Thompson conjecture is a conjecture in number theory, suggested by Walter Feit and John G. Thompson (1962). The conjecture states that there are no distinct prime numbers p and q for which

If the conjecture were true, it would greatly simplify the final chapter of the proof (Feit & Thompson 1963) of the Feit–Thompson theorem that every finite group of odd order is solvable. A stronger (and rather implausible) conjecture that the two numbers are always coprime was disproved by Stephens (1971) with the counterexample p = 17 and q = 3313 with common factor 2pq + 1 = 112643.

Informal probability arguments suggest that the "expected" number of counterexamples to the Feit–Thompson conjecture is very close to 0, suggesting that the Feit–Thompson conjecture is likely to be true.

See also

• Cyclotomic polynomials
• Goormaghtigh conjecture

References

• Feit, Walter; Thompson, John G. (1962), "A solvability criterion for finite groups and some consequences", Proc. Nat. Acad. Sci. U.S.A. 48 (6): 968–970, doi:10.1073/pnas.48.6.968, JSTOR 71265  MR0143802
• Feit, Walter; Thompson, John G. (1963), "Solvability of groups of odd order", Pacific J. Math. 13: 775–1029, ISSN 0030-8730  MR0166261
• Stephens, Nelson M. (1971), "On the Feit–Thompson conjecture", Math. Comp. 25: 625, doi:10.2307/2005226, JSTOR 2005226  MR0297686

External links

• Weisstein, Eric W., "Feit–Thompson Conjecture" from MathWorld. (This article confuses the Feit–Thompson conjecture with the stronger disproved conjecture mentioned above.)